The "Big-Oh" Notation (Data Structure and Algorithms in Python #1002)

-

The “Big-Oh” Notation

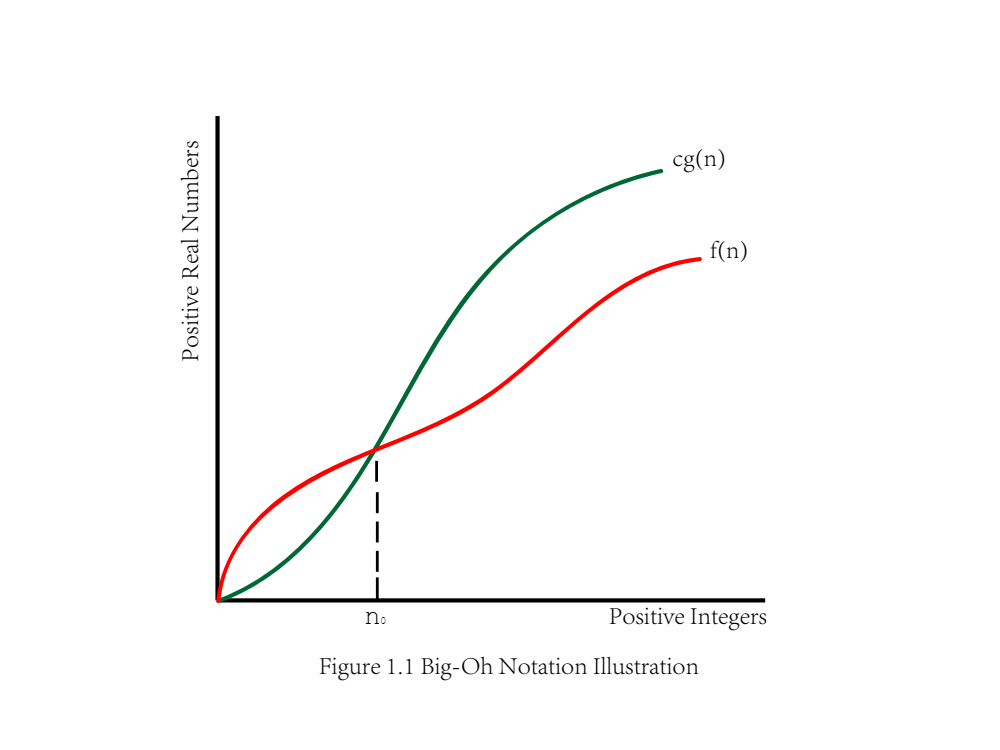
If f(n) and g(n) are two functions that map positive integers to positive real numbers. We could say that f(n) is O(g(n)) if there is a real constant c > 0 and an integer constant n0 > 1 that:
f(n) ≤ cg(n), for n > n0
The f(n) is O(g(n)) is usually read as “f(n) is big-Oh of g(n)”. The following graph illustrates the “Big-Oh” notation.
Example 1.1 Justify the function f(n) = 5n + 3 is O(n)
Answer:
By the definition of “Big-Oh” notation, there must exist a constant c > 0 such that:
f(n) ≤ cg(n) or 5n + 3 ≤ cn for all n > n0 
5n + 3 ≤ (5 + 3)n = 8n and n0 = 1, so 5n + 3 is O(n)

Example 1.2 Justify 5n2 + 2nlogn + 3n + 6 is O(n2) (logn ≤ n for n ≥ 1, base 2)
Answer: 5n2 + 2nlogn + 3n + 6 ≤ (5 + 2 + 3 + 6)n2 = 16n2 for c = 16, when n ≥ n0 = 1

Example 1.3 Justify 2logn + 2 is O(logn) (logn ≤ n for n ≥ 1, base 2)

Answer: 2logn + 2 ≤ (2 + 2)logn = 4logn for c = 4, when n ≥ n0 = 2 for log1 = 0

Comments

New comments are not allowed.

Popular posts from this blog

How to write a slide puzzle game with Python and Pygame (2020 tutorial)

-
Image
Table of Contents Preparation Introduction Import modules and define contants Create the main game screen Creae the data structure of the board Let's draw the tiles The game logic Define the missing functions Preparation In this tutorial, we are gonna use Python 3.8 and Pygame v1.96.  For the installation of Python and Pygame, please follow the documents found on each webiste. Python: https://www.python.org/ Pygame: https://www.pygame.org/ Introduction As you can see from the picture above, we create a board with 15 green tiles and one white tile which represent a empty slot. Our gaol is to place all the 15 green tiles back into its sorted order, namely: A B C D E F G H I J K L  M N O If we click on the tile "F", the tile will slide down south. And if all the tiles are back into their sorted order, you won the game and quit the game. That's pretty much the gist of the game, later you could add other features to the game. Import modules and define contatnts impor
Read more

How to create a memory puzzle game with Python and Pygame (#005)

-
First look at the following code: import time # create Font object text_font = pygame . font . SysFont( 'arial' , 50 ) # create a list that stores two pos that going to compare to each other pos_to_compare_list = [] # create a list that stores all the pos that matched pos_matched = [] # set backgroud color to white while True : for event in pygame . event . get(): if event . type == QUIT: pygame . quit() sys . exit() elif event . type == MOUSEBUTTONDOWN: (x,y) = pygame . mouse . get_pos() pos = check_click(x,y, square_pos) if pos: text_surface = text_font . render(board[pos[ 0 ]][pos[ 1 ]], True , WHITE) if len (pos_to_compare_list) < 2 : if pos not in pos_to_compare_list: pos_to_compare_list . append(pos)
Read more

Introduction to multitasking with Python #001 multithreading (2020 tutorial)

-
Image
1. What is multitasking? So far, we have written so many programs with python. All the instructions inside a program run sequentially one by one. Let's look at an simple example: # multithreading_example01.py # basci program without using threading import time def sing (): for i in range ( 5 ): print ( 'Singing...' ) time . sleep( 1 ) def dance (): for i in range ( 5 ): print ( 'Dancing...' ) time . sleep( 1 ) def main (): # singing a song sing() # dancing dance() if __name__ == '__main__' : main()  After running this program, after ten seconds the program exits. But if we want to dance and sing at the same time intead of doing one after another, what we could do with the code? In python, we could use the threading module and run both sing() and dance functions at the same time. Here is how we can do it: # multithreading_example01.py
Read more