Coding Fun

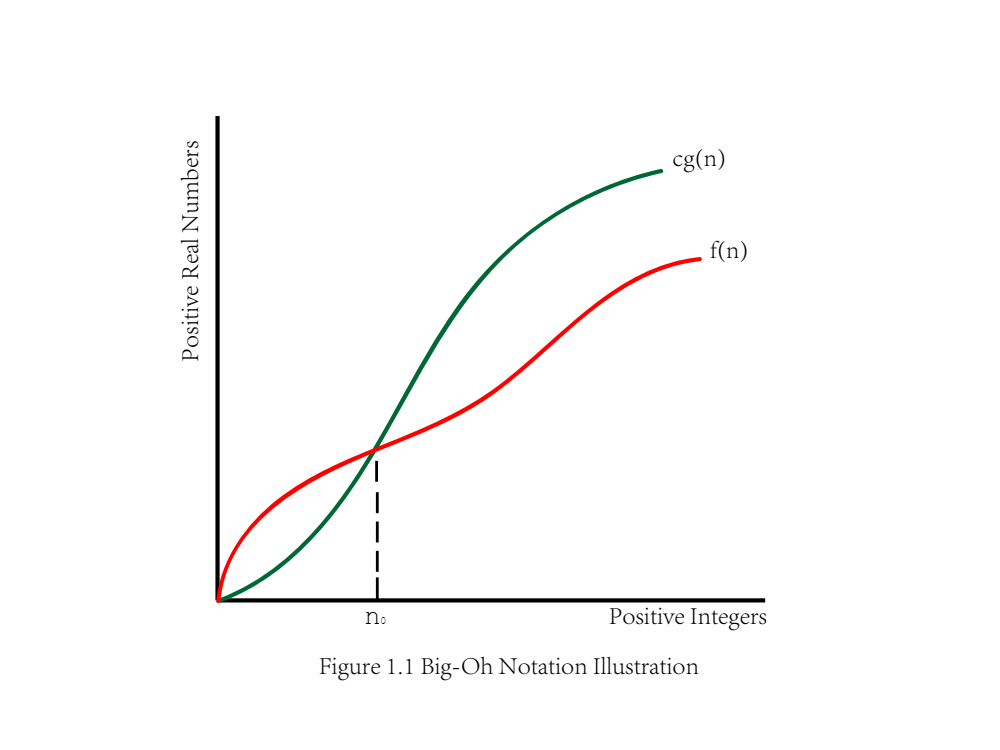
Anaylyzing Algorithms Using The "Big-Oh" Notation Let us design a python program find_max(s) which takes a sequence of numbers as the parameter and computes the maximum element. def find_max(s):     largest = s[0] # assume the first element be the largest     for e in s: # iterate through the sequence         if e > largest:             largest = e  return largest Analysis: when find_max is invoked, the initialization before the for loop requires only a constant number of primitive operations, we denote this constant number c' . For each iteration of the loop, it also requires a constant number of primitive operations, and we denote this number c'' . For the loop executes n times, so we can say the total number of primitive operations can be written as: c' + c''·n . So by the definition of “ Big-Oh ” notati...

The “Big-Oh” Notation If f(n) and g(n) are two functions that map positive integers to positive real numbers. We could say that f(n) is O(g(n)) if there is a real constant c > 0 and an integer constant n 0   > 1 that: f(n) ≤ cg(n), for n > n 0 The f(n) is O(g(n)) is usually read as “ f(n) is big-Oh of g(n) ”.  The following graph illustrates the “ Big-Oh ”  notation. Example 1.1 Justify the function f(n) = 5n + 3 is O(n) Answer: By the definition of “ Big-Oh ” notation, there must exist a constant c > 0 such that: f(n) ≤ cg(n) or 5n + 3 ≤ cn for all n >  n 0  5n + 3 ≤ (5 + 3)n = 8n and n 0 = 1 , so 5n + 3 is O(n) Example 1.2 Justify 5n 2  + 2nlogn + 3n + 6 is O(n 2 ) ( logn ≤ n for n ≥ 1 , base 2 ) Answer: 5n 2  + 2nlogn + 3n + 6 ≤ (5 + 2 + 3 + 6)n 2  = 16n 2  for c = 16 , when n ≥ n 0  = 1 Example 1.3 Justify 2logn + 2 is O(...

Introduction This is the first course of the "Data Structure and Algorithms in Python" series. Before we go deeper on this topic, I would like to introduce the most important math tool that we are gonna use through out this topic " Aysmpotic Analysis ".   What is asymptotic analysis? In mathematics, asymptotic analysis, also known as asymptotics, is a method of describing limiting behaviors. For instance, if we are insterested in the properties of function  f(n)  as n becomes very large. If  f(n) = n 2 + 4n + 3 , as n goes to infinity ( ∞ ), the term 4n and constant 3 becomes insignificant compared to n 2 . And we can say that “ f(n) is asymptotically equivalent to n 2 , as n → ∞ ” . This is often written as f(n)~n 2 , which read as “ f(n) is asymptotic to n 2 ” .